Fisica realizzabilità di un sistema di controllo
--> Clicca qui per la bibliografia
Fisica realizzabilità del controllore |
|
Supponiamo di aver assegnato , a partire dalle specifiche di progetto , una W(s) desiderata per il sistema a ciclo chiuso e di aver calcolato, in base alle relazioni del paragrafo precedente, la F(s) che da luogo a tale f.d.t. Supponiamo che l'andamento in frequenza della F(s) così ottenuta sia quello indicato in figura 1:
|
 |
| Essendo F(s)=P(s)*G(s) nel caso di reazione unitaria e F(s)=G(s)*P(s)*H(s) nel caso di reazione dinamica , anche il controllore G(s) resta automaticamente determinato. Poniamoci ad esempio nel caso di sintesi ad un grado di libertà ed andiamo a considerare la relazione fra i moduli delle f.d.t. in gioco: |
 |
|
e a seconda del processo che dobbiamo controllare, ci possiamo trovare in una delle due seguenti situazioni :
a) l'andamento di |P(jw)| , alle alte frequenze, si trova al di sopra di |F(jw)| ( curva verde in figura 2 ) , quindi G(s) ha un comportamento di tipo passa-basso ed è fisicamente realizzabile. b) l'andamento di |P(jw)| , alle alte frequenze , si trova al di sotto di |F(jw)| ( curva blu in figura 2 ) , quindi G(s) ha un andamento passa alto e non è fisicamente realizzabile. |
 |
|
Si dovrà quindi provvedere ad effettuare preventive verifiche sulla P(s) in modo da non trovarsi nella situazione di fisica irrealizzabilità , modificando eventualmente le aspettative sulla W(s) e/o sulla Wz(s) ( un ragionamento analogo a quello sulla G(s) vale infatti per la K(s) della sintesi a compensazione diretta ). Si può dimostrare che delle condizioni da rispettare per non trovarsi in questa situazione sono :
1)
 per quanto riguarda la W(s) ; m ed n sono rispettivamente il grado del numeratore e del denominatore della funzione di trasferimento a ciclo chiuso , mentre mp ed np sono rispettivamente il grado del numeratore e del denominatore del processo , quindi tale condizione equivale a chiedere che l'eccesso poli-zeri della W(s) sia almeno pari all'eccesso poli-zeri del processo. per quanto riguarda la W(s) ; m ed n sono rispettivamente il grado del numeratore e del denominatore della funzione di trasferimento a ciclo chiuso , mentre mp ed np sono rispettivamente il grado del numeratore e del denominatore del processo , quindi tale condizione equivale a chiedere che l'eccesso poli-zeri della W(s) sia almeno pari all'eccesso poli-zeri del processo. 2)  per quanto riguarda la Wz(s) ; il significato fisico di tale condizione è evidente : non si può chiedere ad un sistema di controllo di attenuare ( |Wz(s)|<1 ) gli effetti del rumore a tutte le frequenze. per quanto riguarda la Wz(s) ; il significato fisico di tale condizione è evidente : non si può chiedere ad un sistema di controllo di attenuare ( |Wz(s)|<1 ) gli effetti del rumore a tutte le frequenze. |




















 , la funzione di trasferimento disturbo/uscita
, la funzione di trasferimento disturbo/uscita  e tenere presente che l'uscita desiderata rispetto al disturbo è nulla (
e tenere presente che l'uscita desiderata rispetto al disturbo è nulla (  ) : si vorrebbe infatti che il sistema di controllo fosse insensibile ai disturbi , che questi , cioè, non producessero alcun effetto sull'uscita.
) : si vorrebbe infatti che il sistema di controllo fosse insensibile ai disturbi , che questi , cioè, non producessero alcun effetto sull'uscita.  .
.




 , vista nel paragrafo precedente , per i sistemi di controllo proporzionali , a partire da diverse possibili espressioni per la funzione di trasferimento W(s) :
, vista nel paragrafo precedente , per i sistemi di controllo proporzionali , a partire da diverse possibili espressioni per la funzione di trasferimento W(s) : . Sviluppando l'equazione della We(s) e portando i due termini a denominatore comune , otteniamo :
. Sviluppando l'equazione della We(s) e portando i due termini a denominatore comune , otteniamo :

 . Si tratta di trovare delle relazioni fra le costanti di tempo dei singoli poli e zeri : trovare una condizione di validità generale per ogni k , a partire dalla proposizione 1 , risulta in questo caso più difficile . Conviene allora , a partire dalle condizioni sui Ce,i trovate nel paragrafo precedente, trovare delle condizioni per ottenere dei sistemi di tipo zero, uno , due, che sono quelli più facili da trovare operativamente.
. Si tratta di trovare delle relazioni fra le costanti di tempo dei singoli poli e zeri : trovare una condizione di validità generale per ogni k , a partire dalla proposizione 1 , risulta in questo caso più difficile . Conviene allora , a partire dalle condizioni sui Ce,i trovate nel paragrafo precedente, trovare delle condizioni per ottenere dei sistemi di tipo zero, uno , due, che sono quelli più facili da trovare operativamente. . In caso contrario il sistema è certamente di tipo k>0.
. In caso contrario il sistema è certamente di tipo k>0. e , per la definizione stessa del guadagno statico :
e , per la definizione stessa del guadagno statico :  . Pertanto perché il coefficiente sia non nullo deve aversi
. Pertanto perché il coefficiente sia non nullo deve aversi 



 , perciò imponendo che Ce,2=0 si ha la 3B.3) .
, perciò imponendo che Ce,2=0 si ha la 3B.3) .

 .
. ) , la funzione di trasferimento del sistema errore si può scrivere come :
) , la funzione di trasferimento del sistema errore si può scrivere come : .
. .
.

 ,
,


 .
.




 .
. all'ingresso a regime
all'ingresso a regime  per una quantità costante non nulla.
per una quantità costante non nulla. 

 da scegliere in base alle costanti di tempo del sistema da analizare ( solitamente 1 rad/s) . Anche l'asse delle ordinate , per il diagramma del modulo , ha scala logaritmica espressa in decibel :
da scegliere in base alle costanti di tempo del sistema da analizare ( solitamente 1 rad/s) . Anche l'asse delle ordinate , per il diagramma del modulo , ha scala logaritmica espressa in decibel :
 in gradi o radianti.
in gradi o radianti.
 ;
;



 ;
; .
.

 , dove si è definito
, dove si è definito  , e:
, e: , per cui il modulo è pressoché nullo
, per cui il modulo è pressoché nullo  e si è visto, analizzando il contributo del derivatore, che tale espressione corrisponde ad una pendenza positiva di 20dB/decade.
e si è visto, analizzando il contributo del derivatore, che tale espressione corrisponde ad una pendenza positiva di 20dB/decade. e :
e :



 , definita dall'equazione
, definita dall'equazione  , come intersezione fra il diagramma della fase e la linea tratteggiata verde in figura ;
, come intersezione fra il diagramma della fase e la linea tratteggiata verde in figura ;  , definita in precedenza come
, definita in precedenza come  , dall'intersezione fra il diagramma del modulo e la linea tratteggiata celeste ( asse delle ascisse del primo diagramma , corrispondente ad una retta a modulo costante 0dB )
, dall'intersezione fra il diagramma del modulo e la linea tratteggiata celeste ( asse delle ascisse del primo diagramma , corrispondente ad una retta a modulo costante 0dB )




 , è una prima possibile definizione del margine di guadagno.
, è una prima possibile definizione del margine di guadagno.


 ;
;





 .
. , ciascuno zero di ordine k contribuisce con la fase
, ciascuno zero di ordine k contribuisce con la fase  , mentre ciascun polo di ordine k contribuisce con la fase
, mentre ciascun polo di ordine k contribuisce con la fase  . Complessivamente, quindi, il diagramma di Nyquist arriva nel punto considerato con la fase
. Complessivamente, quindi, il diagramma di Nyquist arriva nel punto considerato con la fase ,
, . Se invece gli integratori sono due, il diagramma partirà da un punto che diverge verso la direzione negativa dell'asse reale , ecc ;
. Se invece gli integratori sono due, il diagramma partirà da un punto che diverge verso la direzione negativa dell'asse reale , ecc ; : questo punto permette infatti di intuire in che direzione muove il diagramma di Nyquist per andare dalla frequenza nulla a frequenza infinita. Se non si vuole calcolare esplicitamente il limite , è sufficiente tenere conto delle costanti di tempo di poli e zeri della f.d.t. e valutare il modulo per una frequenza che corrisponda ad un tempo sufficientemente maggiore della costante di tempo più grande.
: questo punto permette infatti di intuire in che direzione muove il diagramma di Nyquist per andare dalla frequenza nulla a frequenza infinita. Se non si vuole calcolare esplicitamente il limite , è sufficiente tenere conto delle costanti di tempo di poli e zeri della f.d.t. e valutare il modulo per una frequenza che corrisponda ad un tempo sufficientemente maggiore della costante di tempo più grande.
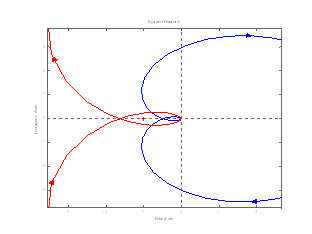
 : il diagramma di Nyquist alle alte frequenze tende all'origine del piano caratteristico e vi arriva tangente al semiasse immaginario negativo, come mostra la figura 1.
: il diagramma di Nyquist alle alte frequenze tende all'origine del piano caratteristico e vi arriva tangente al semiasse immaginario negativo, come mostra la figura 1.

 ; si può quindi costruire sperimentalmente osservando la risposta in frequenza della catena di blocchi che costituiscono l'anello aperto del sistema di controllo.
; si può quindi costruire sperimentalmente osservando la risposta in frequenza della catena di blocchi che costituiscono l'anello aperto del sistema di controllo.  e quello in catena aperta
e quello in catena aperta 
 la funzione di trasferimento sul ramo diretto, si avrà che la f.d.t in catena aperta è
la funzione di trasferimento sul ramo diretto, si avrà che la f.d.t in catena aperta è  e la f.d.t. a ciclo chiuso è
e la f.d.t. a ciclo chiuso è  .
.  il denominatore della W(s) , cioè il polinomio caratteristico a ciclo chiuso. In base a questa definizione, quando si va a calcolare 1+F(s) , si ottiene proprio :
il denominatore della W(s) , cioè il polinomio caratteristico a ciclo chiuso. In base a questa definizione, quando si va a calcolare 1+F(s) , si ottiene proprio :  .
. e con Zch il numero di radici a parte reale positiva di
e con Zch il numero di radici a parte reale positiva di 

 .
. e
e  ha riassunto il valore iniziale , come mostrato in figura 2. I poli e gli zeri esterni alla curva C non danno quindi contributo alla variazione della fase di G(s) sul piano immagine, al termine di un giro completo.
ha riassunto il valore iniziale , come mostrato in figura 2. I poli e gli zeri esterni alla curva C non danno quindi contributo alla variazione della fase di G(s) sul piano immagine, al termine di un giro completo.
 .
.

